Function Spaces¶
Once we have created a grid, we can define finite-dimensional function spaces on the grid. These spaces will then be used to discretise the boundary integral formulations of our problem.
Full documentation of Bempp function spaces can be found on Read the Docs.
Defining a function space¶
The function function_space is used to initialise spaces. To define
a space of piecewise constant functions we use the command:
space = bempp.api.function_space(grid, "DP", 0)
The parameter DP is short for Discontinuous Polynomial. The number 0 is
the degree of the polynomial space. To define a space of continuous, piecewise
linear functions use:
space = bempp.api.function_space(grid, "P", 1)
Bempp-cl only supports function spaces up to degree 1. This is an important difference to earlier versions that also supported higher order spaces.
The number of degrees of freedom (DOFs) in a space can be found using:
space.global_dof_count
For solving Laplace or Helmholtz problems, scalar function spaces should be used. For solving Maxwell’s equations, vector function spaces should be used.
Scalar Function Spaces¶
The following scalar-valued spaces are supported in Bempp:
Space Type |
Order(s) |
Description |
|---|---|---|
|
0 or 1 |
Discontinuous polynomials |
|
1 |
Continuous polynomials |
|
0 or 1 |
Dual spaces on the barycentrically refined grid |
Discontinuous polynomial spaces¶
DP spaces are polynomial inside each element and discontinuous between elements. An example basis function of an order 0 DP space is shown in Fig. 1.
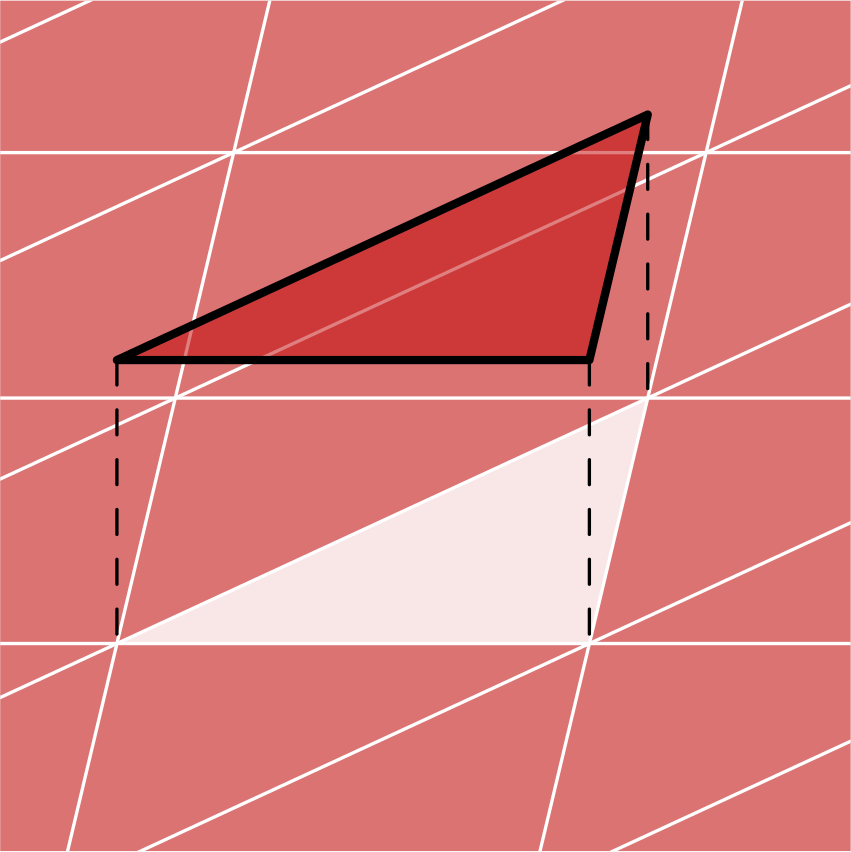
Fig. 1 Discontinuous polynomial order 0 basis function¶
These spaces can be created in Bempp with:
space = bempp.api.function_space(grid, "DP", 0)
space = bempp.api.function_space(grid, "DP", 1)
The DOFs of an order 0 DP space are at the midpoints of each cell. The DOFs of an order 1 DP space are at the three vertices of each cell.
Continuous polynomial spaces¶
P spaces are polynomial inside each element and continuous between elements. An example basis function of an order 1 P space is shown in Fig. 2.
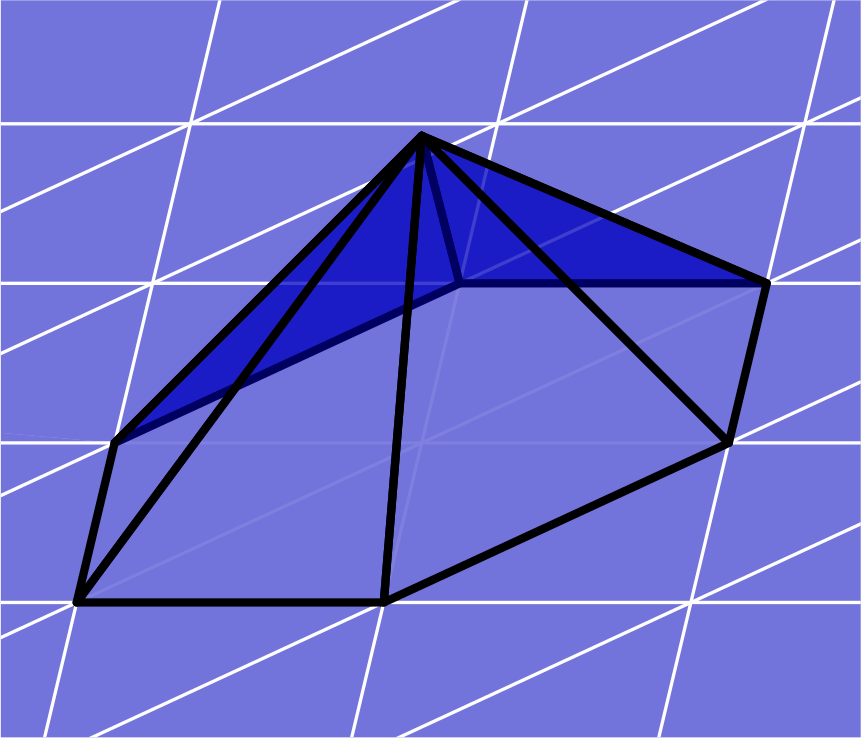
Fig. 2 Continuous polynomial order 1 basis function¶
This space can be created in Bempp with:
space = bempp.api.function_space(grid, "P", 1)
The DOFs of an order 1 P space are at the three vertices of each cell.
Barycentric dual spaces¶
To define the barycentric dual space, we first create the barycentrically refined mesh by joining each vertex of every triangle with the centre of the opposite side, as shown in Fig. 3.

Fig. 3 Barycentrically refining a grid¶
The order 0 dual spaces are piecewise constant functions on the dual cells. An example basis function of an order 0 DUAL space is shown in Fig. 4. Order 0 DUAL spaces form a stable dual pairing with order 1 P spaces.
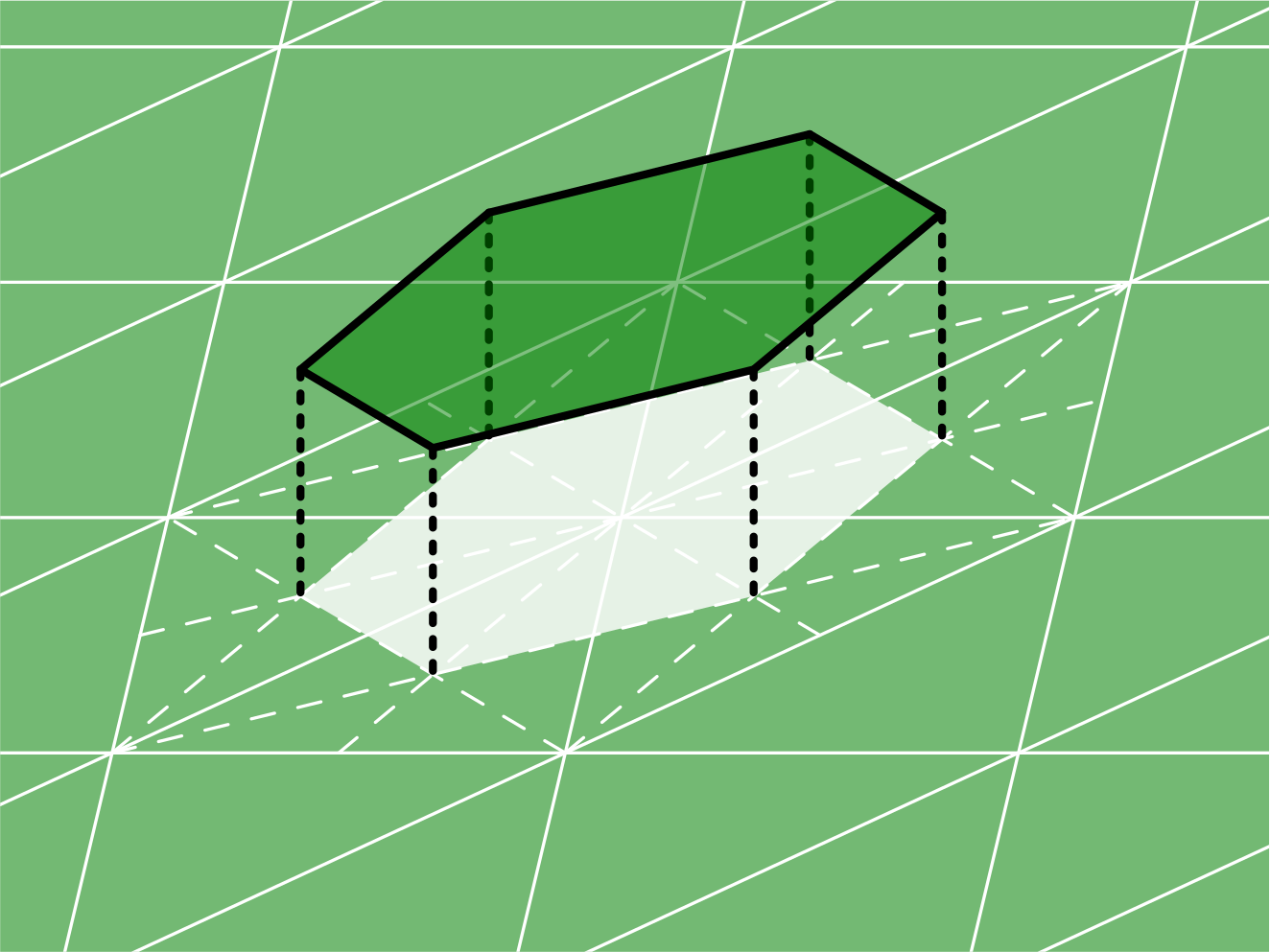
Fig. 4 Dual order 0 basis function¶
The order 1 dual basis functions are linear combinations of piecewise linear functions on the barycentric cells, and are defined in A dual finite element complex on the barycentric refinement (2007) by A. Buffa and S. Christiansen. An example basis function of an order 1 DUAL space is shown in Fig. 5. Order 1 DUAL spaces form a stable dual pairing with order 0 DP spaces.
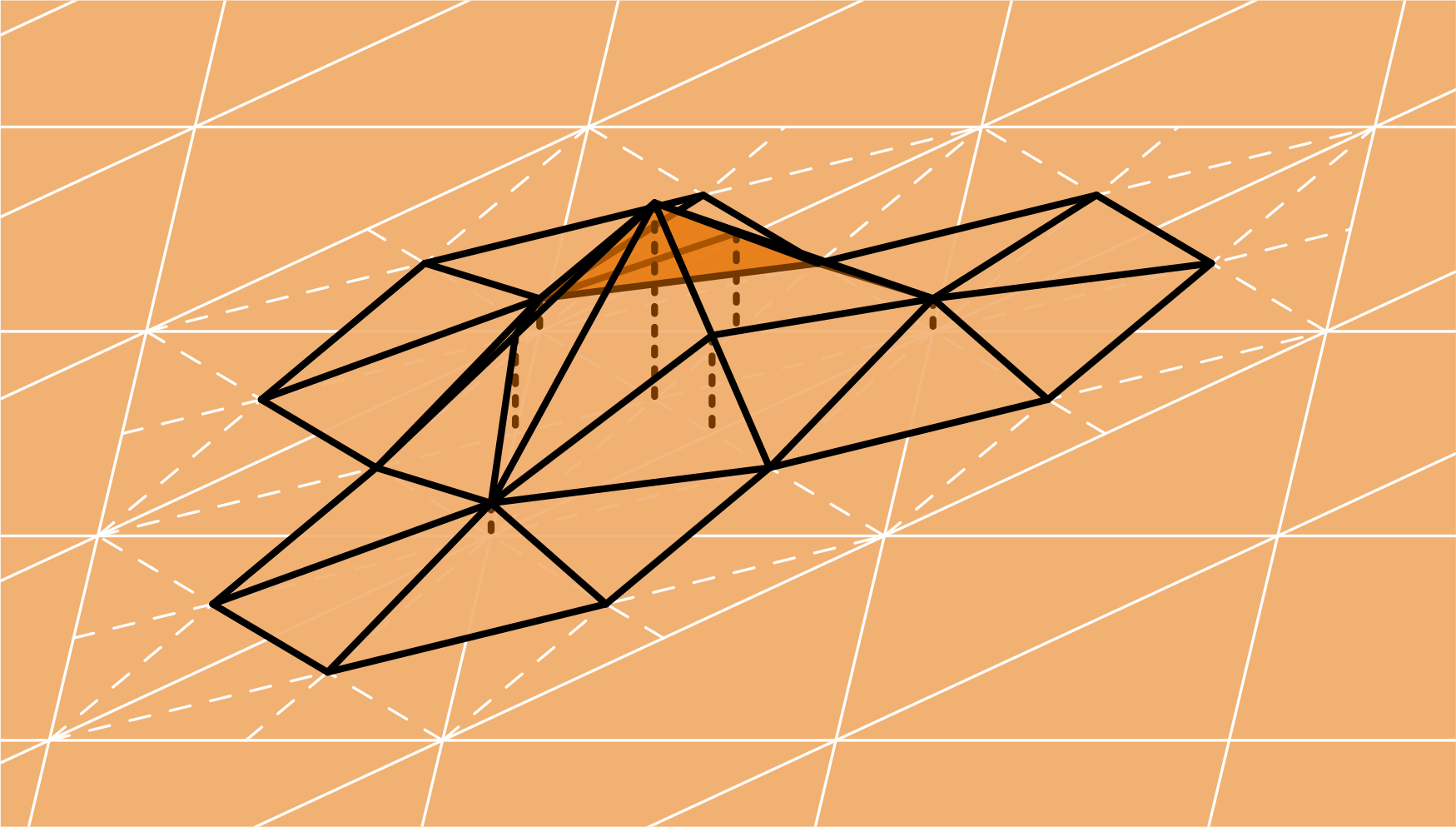
Fig. 5 Dual order 1 basis function¶
These spaces can be created in Bempp with:
space = bempp.api.function_space(grid, "DUAL", 0)
space = bempp.api.function_space(grid, "DUAL", 1)
The DOFs of an order 0 DUAL space are at the three vertices of each cell (ie the midpoints of each barycentric dual cell). The DOFs of an order 1 DUAL space are at the mispoints of each cell (ie the vertices of each barycentric dual cell).
Vector Function Spaces¶
The following vector-valued spaces are supported in Bempp:
Space Type |
Order |
Description |
|---|---|---|
|
0 |
Rao–Wilson–Glisson Hdiv functions |
|
0 |
Scaled Nédélec Hcurl functions |
|
0 |
Buffa–Christiansen Hdiv functions |
|
0 |
Rotated Buffa–Christiansen Hcurl functions |
When solving Maxwell’s equations, the correct combination of Hdiv and Hcurl spaces must be used.
RWG and SNC spaces¶
RWG and SNC spaces are vector-valued spaces, whose values are tangential to the surface triangles. Between cells, RWG functions are continuous normal to the triangle’s edges, while SNC spaces are continuous tangential to the triangle’s edges. Example RWG (left) and SNC (right) basis functions are shown in Fig. 6.
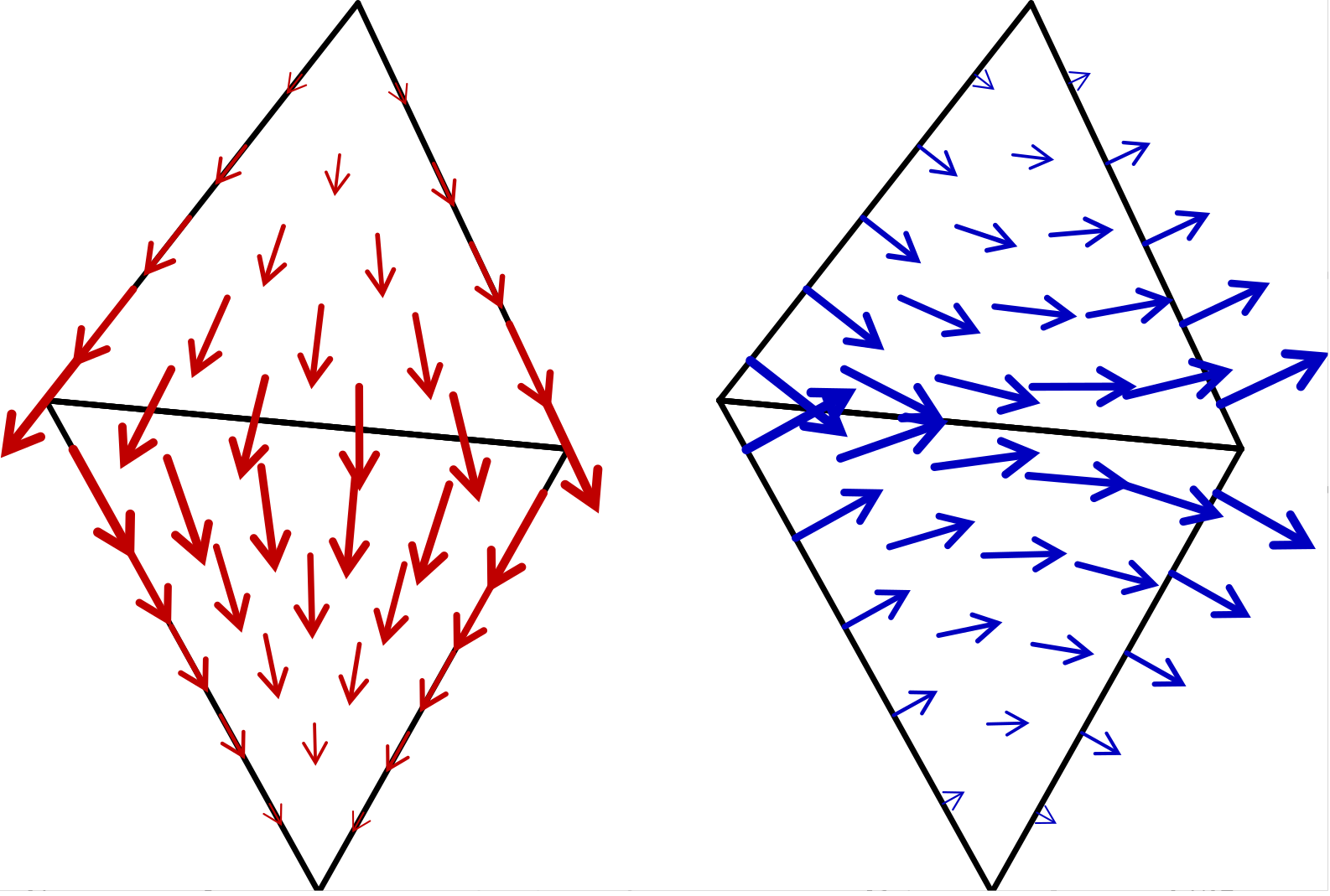
Fig. 6 An RWG and a SNC basis function¶
These spaces can be created in Bempp with:
rwg_space = bempp.api.function_space(grid, "RWG", 0)
snc_space = bempp.api.function_space(grid, "SNC", 0)
The DOFs of RWG and SNC spaces are at the midpoints of the edges of each cell.
Barycentric dual spaces¶
Like the scalar DUAL spaces, BC and RBC spaces are defined on the barycentrically refined grid. This grid is formed by joining each vertex of every triangle with the centre of the opposite side, as shown in Fig. 3.
BC and RBC spaces are combinations of RWG and SNC (repectively) spaces on the barycentric grid, and are defined in A dual finite element complex on the barycentric refinement (2007) by A. Buffa and S. Christiansen. Example BC (left) and RBC (right) basis functions are shown in Fig. 7.
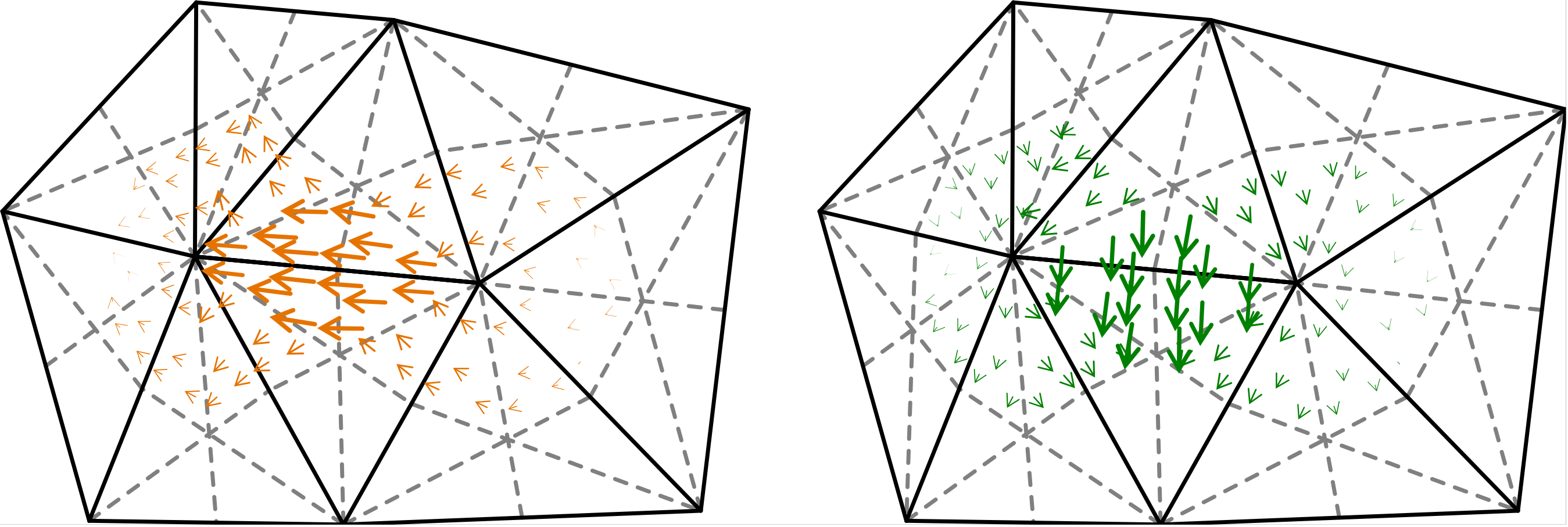
Fig. 7 A BC and a RBC basis function¶
These spaces can be created in Bempp with:
bc_space = bempp.api.function_space(grid, "BC", 0)
rbc_space = bempp.api.function_space(grid, "RBC", 0)
The DOFs of BC and RBC spaces are at the midpoints of the edges of each cell (or equivalently at a point on the edges of the barycentric dual cells).
Function Spaces on Segments¶
Bempp can create spaces on segments of a grid as well as on the entire grid. In order to do this, domain indices must be provided when [creating .md). Some built-in grids have domain indices: for example, the cube has six segments for the faces (numbered 1 to 6).
To create a space on a segment, first create the grid:
grid = bempp.api.shapes.cube()
A space on segments 1 and 2 of the grid can then be created using:
space = bempp.api.function_space(grid, "DP", 0, segments=[1, 2])
Controlling segment spaces¶
There are two options that can be used to control the behaviour of a space on a segment:
include_boundary_dofs and truncate_at_segment_edge.
If include_boundary_dofs is set to True, DOF points on vertices and edges on the boundary.
By default, this is set to False. Setting this option to True is likely to make the
function space extend outside its segments, as part of the basis functions with DOFs on the
boundary will be outside the domain.
The option truncate_at_segment_edge can be used to truncate basis functions at the edge of the
segment, whenever a basis function will extend outside the segments. By default, this is False.
Setting this option to True will cause the function space to be discontinuous at the edge
of the segment.